CNN Demonstration¶
The Model¶
We train CNN model to predict nino3.4 index
Running the CNN Model¶
Set up python packages including xarray, sklearn, and torch.
Put these files under the same folder:
enso_prediction_mlo.py
nino34.long.anom.data.txt
Python Script¶
Import packages and functions
import xarray as xr
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
import sklearn
import sklearn.ensemble
import scipy.stats
from sklearn.model_selection import train_test_split
from tqdm import tqdm
import xarray as xr
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
import sklearn
import sklearn.ensemble
import scipy.stats
from sklearn.model_selection import train_test_split
import torch
#import torchvision
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.utils.data import Dataset, DataLoader
from scipy.stats import pearsonr
from sklearn.metrics import mean_squared_error
Define functions
def load_enso_indices():
"""
Reads in the txt data file to output a pandas Series of ENSO vals
outputs
-------
pd.Series : monthly ENSO values starting from 1870-01-01
"""
with open('nino34.long.anom.data.txt') as f:
line = f.readline()
enso_vals = []
while line:
yearly_enso_vals = map(float, line.split()[1:])
enso_vals.extend(yearly_enso_vals)
line = f.readline()
enso_vals = pd.Series(enso_vals)
enso_vals.index = pd.date_range('1870-01-01',freq='MS',
periods=len(enso_vals))
enso_vals.index = pd.to_datetime(enso_vals.index)
return enso_vals
def assemble_predictors_predictands(start_date, end_date, lead_time,
dataset, data_format,
num_input_time_steps=1,
use_pca=False, n_components=32,
lat_slice=None, lon_slice=None):
"""
inputs
------
start_date str : the start date from which to extract sst
end_date str : the end date
lead_time str : the number of months between each sst
value and the target Nino3.4 Index
dataset str : 'observations' 'CNRM' or 'MPI'
data_format str : 'spatial' or 'flatten'. 'spatial' preserves
the lat/lon dimensions and returns an
array of shape (num_samples, num_input_time_steps,
lat, lon). 'flatten' returns an array of shape
(num_samples, num_input_time_steps*lat*lon)
num_input_time_steps int : the number of time steps to use for each
predictor sample
use_pca bool : whether or not to apply principal components
analysis to the sst field
n_components int : the number of components to use for PCA
lat_slice slice: the slice of latitudes to use
lon_slice slice: the slice of longitudes to use
outputs
-------
Returns a tuple of the predictors (np array of sst temperature anomalies)
and the predictands (np array the ENSO index at the specified lead time).
"""
file_name = {'observations' : 'sst.mon.mean.trefadj.anom.1880to2018.nc',
'CNRM' : 'CNRM_tas_anomalies_regridded.nc',
'MPI' : 'MPI_tas_anomalies_regridded.nc'}[dataset]
variable_name = {'observations' : 'sst',
'CNRM' : 'tas',
'MPI' : 'tas'}[dataset]
ds = xr.open_dataset(file_name)
sst = ds[variable_name].sel(time=slice(start_date, end_date))
if lat_slice is not None:
"""YOUR CODE HERE"""
raise NotImplementedError("In EXERCISE 7, you must implement the slicing!")
if lon_slice is not None:
"""YOUR CODE HERE"""
raise NotImplementedError("In EXERCISE 7, you must implement the slicing!")
num_samples = sst.shape[0]
#sst is a (num_samples, lat, lon) array
#the line below converts it to (num_samples, num_input_time_steps, lat, lon)
sst = np.stack([sst.values[n-num_input_time_steps:n] for n in range(num_input_time_steps,
num_samples+1)])
#CHALLENGE: CAN YOU IMPLEMENT THE ABOVE LINE WITHOUT A FOR LOOP?
num_samples = sst.shape[0]
sst[np.isnan(sst)] = 0
if data_format=='flatten':
#sst is a 3D array: (time_steps, lat, lon)
#in this tutorial, we will not be using ML models that take
#advantage of the spatial nature of global temperature
#therefore, we reshape sst into a 2D array: (time_steps, lat*lon)
#(At each time step, there are lat*lon predictors)
sst = sst.reshape(num_samples, -1)
#Use Principal Components Analysis, also called
#Empirical Orthogonal Functions, to reduce the
#dimensionality of the array
if use_pca:
pca = sklearn.decomposition.PCA(n_components=n_components)
pca.fit(sst)
X = pca.transform(sst)
else:
X = sst
else: # data_format=='spatial'
X = sst
start_date_plus_lead = pd.to_datetime(start_date) + \
pd.DateOffset(months=lead_time+num_input_time_steps-1)
end_date_plus_lead = pd.to_datetime(end_date) + \
pd.DateOffset(months=lead_time)
if dataset == 'observations':
y = load_enso_indices()[slice(start_date_plus_lead,
end_date_plus_lead)]
else: #the data is from a GCM
X = X.astype(np.float32)
#The Nino3.4 Index is composed of three month rolling values
#Therefore, when calculating the Nino3.4 Index in a GCM
#we have to extract the two months prior to the first target start date
target_start_date_with_2_month = start_date_plus_lead - pd.DateOffset(months=2)
subsetted_ds = ds[variable_name].sel(time=slice(target_start_date_with_2_month,
end_date_plus_lead))
#Calculate the Nino3.4 index
y = subsetted_ds.sel(lat=slice(5,-5), lon=slice(360-170,360-120)).mean(dim=('lat','lon'))
y = pd.Series(y.values).rolling(window=3).mean()[2:].values
y = y.astype(np.float32)
ds.close()
return X.astype(np.float32), y.astype(np.float32)
def plot_nino_time_series(y, predictions, title):
"""
inputs
------
y pd.Series : time series of the true Nino index
predictions np.array : time series of the predicted Nino index (same
length and time as y)
titile : the title of the plot
outputs
-------
None. Displays the plot
"""
predictions = pd.Series(predictions, index=y.index)
predictions = predictions.sort_index()
y = y.sort_index()
plt.plot(y, label='Ground Truth')
plt.plot(predictions, '--', label='ML Predictions')
plt.legend(loc='best')
plt.title(title)
plt.ylabel('Nino3.4 Index')
plt.xlabel('Date')
plt.show()
plt.close()
class ENSODataset(Dataset):
def __init__(self, predictors, predictands):
self.predictors = predictors
self.predictands = predictands
assert self.predictors.shape[0] == self.predictands.shape[0], \
"The number of predictors must equal the number of predictands!"
def __len__(self):
return self.predictors.shape[0]
def __getitem__(self, idx):
return self.predictors[idx], self.predictands[idx]
Determine network structure
class CNN(nn.Module):
def __init__(self, num_input_time_steps=1, print_feature_dimension=False):
"""
inputs
-------
num_input_time_steps (int) : the number of input time
steps in the predictor
print_feature_dimension (bool) : whether or not to print
out the dimension of the features
extracted from the conv layers
"""
super(CNN, self).__init__()
self.conv1 = nn.Conv2d(num_input_time_steps, 6, 3)
self.pool = nn.MaxPool2d(2, 2)
self.conv2 = nn.Conv2d(6, 16, 5)
self.print_layer = Print()
#ATTENTION EXERCISE 9: print out the dimension of the extracted features from
#the conv layers for setting the dimension of the linear layer!
#Using the print_layer, we find that the dimensions are
#(batch_size, 16, 42, 87)
self.fc1 = nn.Linear(16 * 42 * 87, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 1)
self.print_feature_dimension = print_feature_dimension
def forward(self, x):
x = self.pool(F.relu(self.conv1(x)))
x = self.pool(F.relu(self.conv2(x)))
if self.print_feature_dimension:
x = self.print_layer(x)
x = x.view(-1, 16 * 42 * 87)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
class Print(nn.Module):
"""
This class prints out the size of the features
"""
def forward(self, x):
print(x.size())
return x
CNN training
def train_network(net, criterion, optimizer, trainloader, testloader,
experiment_name, num_epochs=40):
"""
inputs
------
net (nn.Module) : the neural network architecture
criterion (nn) : the loss function (i.e. root mean squared error)
optimizer (torch.optim) : the optimizer to use update the neural network
architecture to minimize the loss function
trainloader (torch.utils.data.DataLoader): dataloader that loads the
predictors and predictands
for the train dataset
testloader (torch.utils.data. DataLoader): dataloader that loads the
predictors and predictands
for the test dataset
outputs
-------
predictions (np.array), and saves the trained neural network as a .pt file
"""
device = "cuda:0" if torch.cuda.is_available() else "cpu"
net = net.to(device)
best_loss = np.infty
train_losses, test_losses = [], []
for epoch in range(num_epochs):
for mode, data_loader in [('train', trainloader), ('test', testloader)]:
#Set the model to train mode to allow its weights to be updated
#while training
if mode == 'train':
net.train()
#Set the model to eval model to prevent its weights from being updated
#while testing
elif mode == 'test':
net.eval()
running_loss = 0.0
for i, data in enumerate(data_loader):
# get a mini-batch of predictors and predictands
batch_predictors, batch_predictands = data
batch_predictands = batch_predictands.to(device)
batch_predictors = batch_predictors.to(device)
# zero the parameter gradients
optimizer.zero_grad()
#calculate the predictions of the current neural network
predictions = net(batch_predictors).squeeze()
#quantify the quality of the predictions using a
#loss function (aka criterion) that is differentiable
loss = criterion(predictions, batch_predictands)
if mode == 'train':
#the 'backward pass: calculates the gradients of each weight
#of the neural network with respect to the loss
loss.backward()
#the optimizer updates the weights of the neural network
#based on the gradients calculated above and the choice
#of optimization algorithm
optimizer.step()
#Save the model weights that have the best performance!
running_loss += loss.item()
if running_loss < best_loss and mode == 'test':
best_loss = running_loss
torch.save(net, '{}.pt'.format(experiment_name))
print('{} Set: Epoch {:02d}. loss: {:3f}'.format(mode, epoch+1, \
running_loss/len(data_loader)))
if mode == 'train':
train_losses.append(running_loss/len(data_loader))
else:
test_losses.append(running_loss/len(data_loader))
net = torch.load('{}.pt'.format(experiment_name))
net.eval()
net.to(device)
#the remainder of this notebook calculates the predictions of the best
#saved model
predictions = np.asarray([])
for i, data in enumerate(testloader):
batch_predictors, batch_predictands = data
batch_predictands = batch_predictands.to(device)
batch_predictors = batch_predictors.to(device)
batch_predictions = net(batch_predictors).squeeze()
#Edge case: if there is 1 item in the batch, batch_predictions becomes a float
#not a Tensor. the if statement below converts it to a Tensor
#so that it is compatible with np.concatenate
if len(batch_predictions.size()) == 0:
batch_predictions = torch.Tensor([batch_predictions])
predictions = np.concatenate([predictions, batch_predictions.detach().cpu().numpy()])
return predictions, train_losses, test_losses
Main script begins
#Assemble numpy arrays corresponding to predictors and predictands
train_start_date = '1960-01-01'
train_end_date = '2005-12-31'
num_input_time_steps = 1
lead_time = 1
train_predictors, train_predictands = assemble_predictors_predictands(train_start_date,
train_end_date, lead_time, 'observations', 'spatial', num_input_time_steps=num_input_time_steps)
test_predictors, test_predictands = assemble_predictors_predictands('2007-01-01',
'2017-12-31', lead_time, 'observations', 'spatial', num_input_time_steps=num_input_time_steps)
#Convert the numpy ararys into ENSODataset, which is a subset of the
#torch.utils.data.Dataset class. This class is compatible with
#the torch dataloader, which allows for data loading for a CNN
train_dataset = ENSODataset(train_predictors, train_predictands)
test_dataset = ENSODataset(test_predictors, test_predictands)
#Create a torch.utils.data.DataLoader from the ENSODatasets() created earlier!
#the similarity between the name DataLoader and Dataset in the pytorch API is unfortunate...
trainloader = DataLoader(train_dataset, batch_size=10)
testloader = DataLoader(test_dataset, batch_size=10)
net = CNN(num_input_time_steps=num_input_time_steps)
optimizer = optim.Adam(net.parameters(), lr=0.0001)
experiment_name = "twolayerCNN_{}_{}".format(train_start_date, train_end_date)
predictions, train_losses, test_losses = train_network(net, nn.MSELoss(),
optimizer, trainloader, testloader, experiment_name)
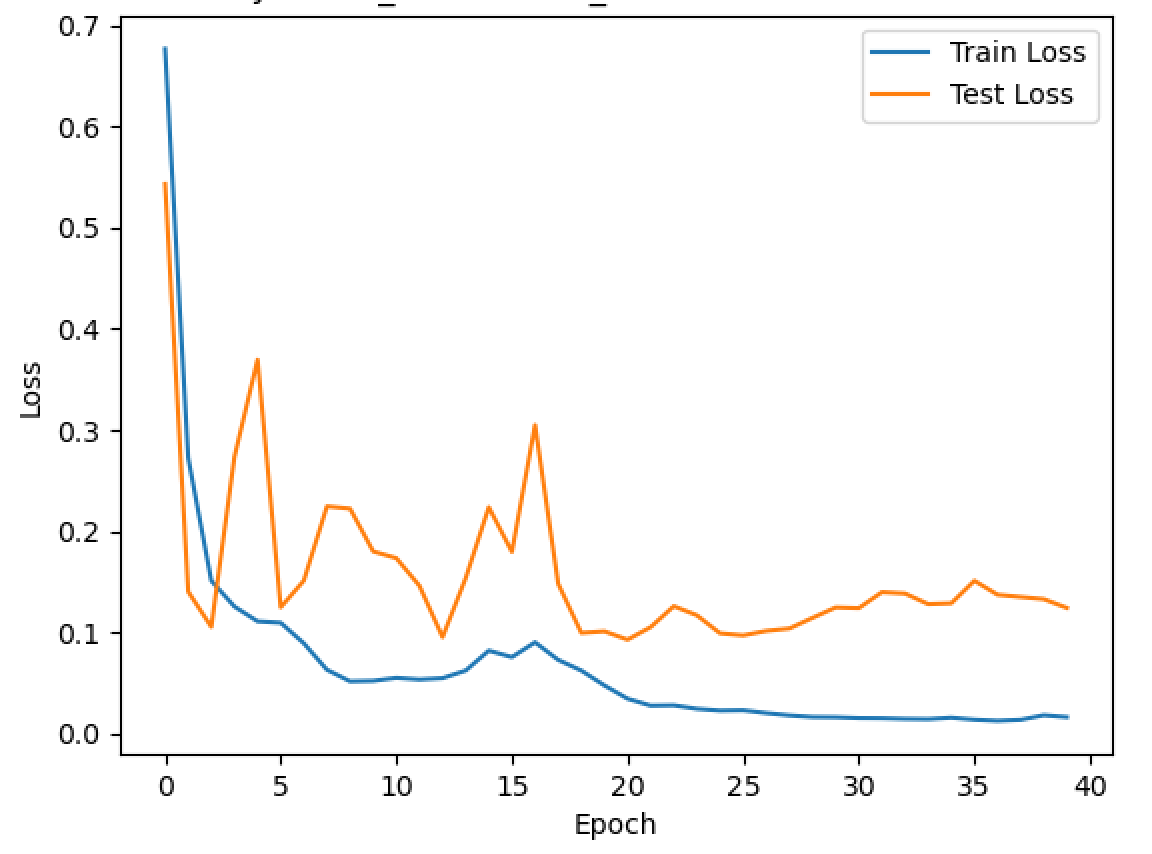
plt.plot(train_losses, label='Train Loss')
plt.plot(test_losses, label='Test Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Performance of {} Neural Network During Training'.format(experiment_name))
plt.legend(loc='best')
plt.show()
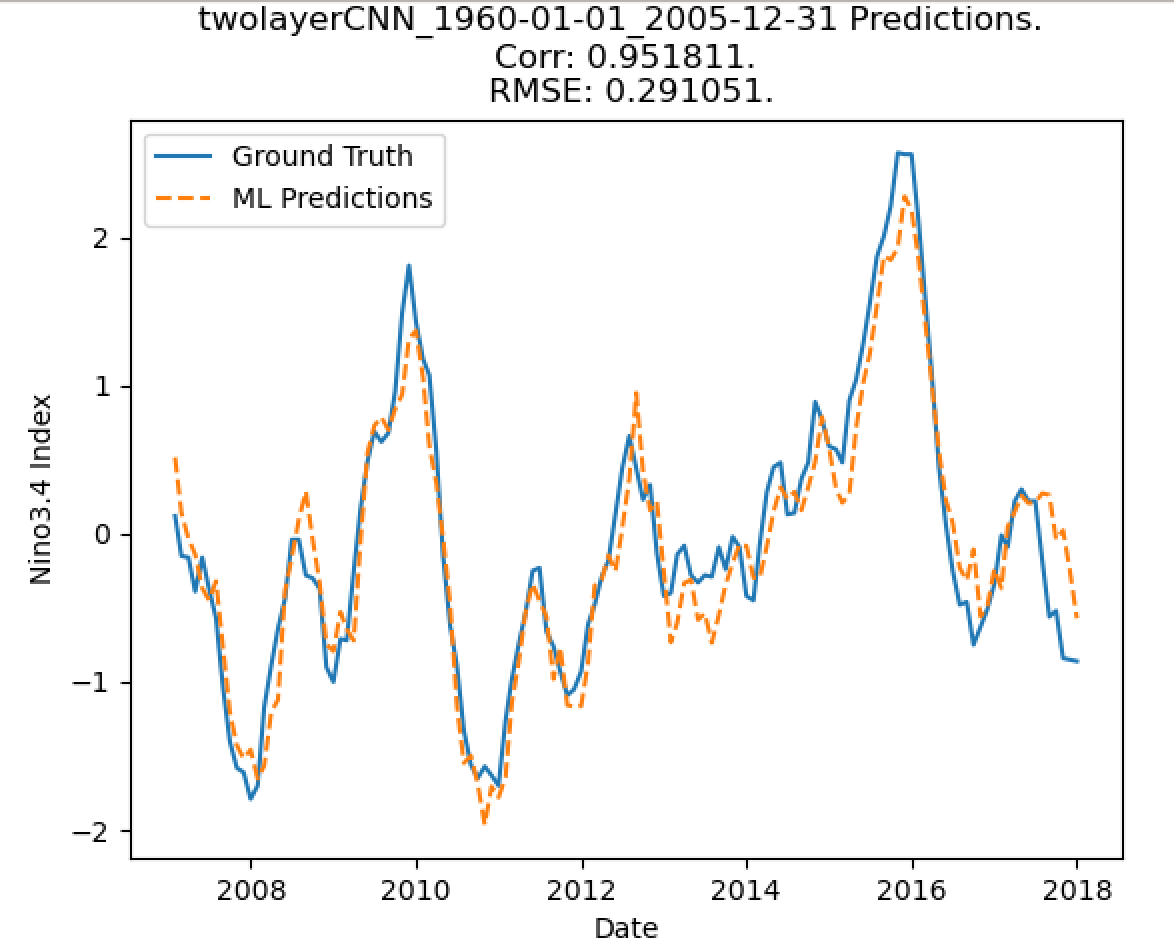
corr, _ = pearsonr(test_predictands, predictions)
rmse = mean_squared_error(test_predictands, predictions) ** 0.5
plot_nino_time_series(test_predictands, predictions, '{} Predictions. \n Corr: {:3f}. \n RMSE: {:3f}.'.format(experiment_name,
corr, rmse))
Validation¶
Predictied Nino3.4 Index¶
Courtesy¶
This code was modified from Glenn Liu’s NCAR Hackthorn project.