15. Seasonal cycle#
Note
The Python scripts used below and some materials are modified from Prof. Brian E. J. Rose’s climlab website.
Seasonal cycle of surface air temperature from reanalysis data#
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import xarray as xr
import climlab
from climlab import constants as const
import cartopy.crs as ccrs # use cartopy to make some maps
ncep_url = "/Users/yuchiaol_ntuas/Desktop/ebooks/data/"
#ncep_url = "http://psl.noaa.gov/thredds/dodsC/Datasets/ncep.reanalysis.derived/"
ncep_Ts = xr.open_dataset(ncep_url + "skt.sfc.mon.1981-2010.ltm.nc", decode_times=False)
# Alternative source from the University of Hawai'i
#url = "http://apdrc.soest.hawaii.edu:80/dods/public_data/Reanalysis_Data/NCEP/NCEP/clima/"
#ncep_Ts = xr.open_dataset(url + 'surface_gauss/skt')
lat_ncep = ncep_Ts.lat; lon_ncep = ncep_Ts.lon
Ts_ncep = ncep_Ts.skt
print( Ts_ncep.shape)
maxTs = Ts_ncep.max(dim='time')
minTs = Ts_ncep.min(dim='time')
meanTs = Ts_ncep.mean(dim='time')
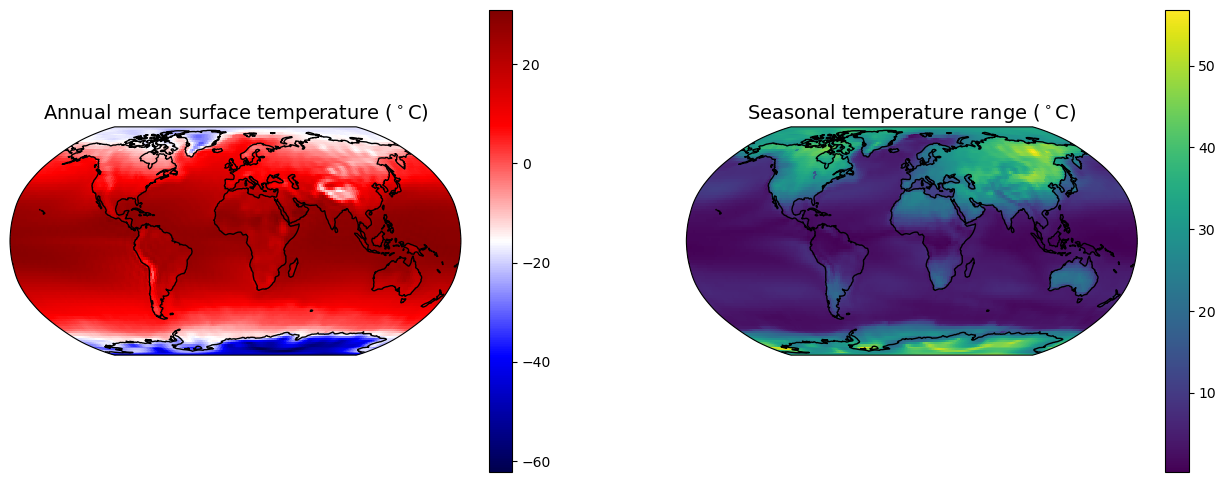
fig = plt.figure( figsize=(16,6) )
ax1 = fig.add_subplot(1,2,1, projection=ccrs.Robinson())
cax1 = ax1.pcolormesh(lon_ncep, lat_ncep, meanTs, cmap=plt.cm.seismic , transform=ccrs.PlateCarree())
cbar1 = plt.colorbar(cax1)
ax1.set_title('Annual mean surface temperature ($^\circ$C)', fontsize=14 )
ax2 = fig.add_subplot(1,2,2, projection=ccrs.Robinson())
cax2 = ax2.pcolormesh(lon_ncep, lat_ncep, maxTs - minTs, transform=ccrs.PlateCarree() )
cbar2 = plt.colorbar(cax2)
ax2.set_title('Seasonal temperature range ($^\circ$C)', fontsize=14)
for ax in [ax1,ax2]:
#ax.contour( lon_cesm, lat_cesm, topo.variables['LANDFRAC'][:], [0.5], colors='k');
#ax.set_xlabel('Longitude', fontsize=14 ); ax.set_ylabel('Latitude', fontsize=14 )
ax.coastlines()
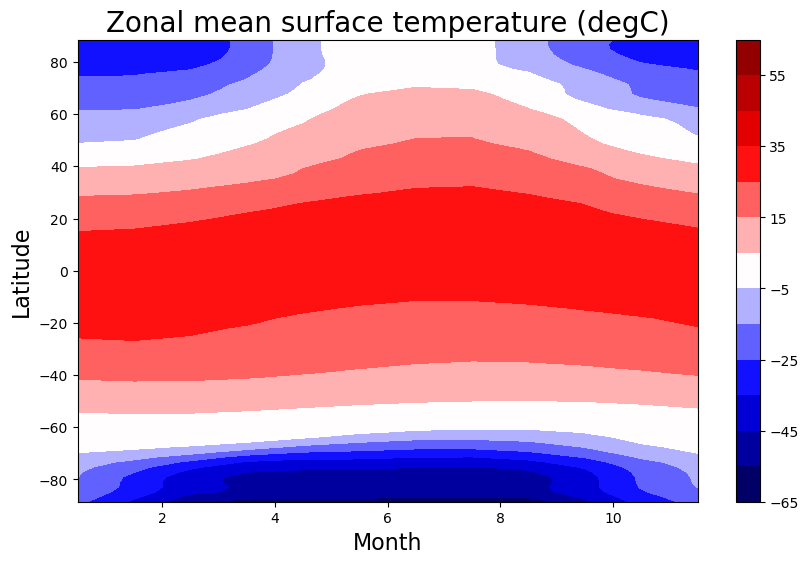
Tmax = 65; Tmin = -Tmax; delT = 10
clevels = np.arange(Tmin,Tmax+delT,delT)
fig_zonobs, ax = plt.subplots( figsize=(10,6) )
cax = ax.contourf(np.arange(12)+0.5, lat_ncep,
Ts_ncep.mean(dim='lon').transpose(), levels=clevels,
cmap=plt.cm.seismic, vmin=Tmin, vmax=Tmax)
ax.set_xlabel('Month', fontsize=16)
ax.set_ylabel('Latitude', fontsize=16 )
cbar = plt.colorbar(cax)
ax.set_title('Zonal mean surface temperature (degC)', fontsize=20)
(12, 94, 192)
Text(0.5, 1.0, 'Zonal mean surface temperature (degC)')
Analytical model#
We consider a simple model:
(152)#\[C\frac{dT}{dt} = Q - (A+BT)\]
We have solar insolation with seasonal cycle:
(153)#\[Q = Q^{*}\sin(\omega t) + Q_{0}\]
where \(\omega = 2\pi\)/year, \(Q_{0}\) is the annual mean insolation.
\(\omega t = 0\) is spring equinox
\(\omega t = \pi /2\) is summer solstice
\(\omega t = \pi\) is fall equinox
\(\omega t = 3\pi/2\) is winter solstice
We seek solution in the form of:
(154)#\[T(t) = T_{0} + T^{*}\sin (\omega t - \Phi)\]
We can determin \(T_0\) by integrating the equation for one year:
(155)#\[\bar{T} = T_{0} \rightarrow Q_{0} = A+B\bar{T} \rightarrow T_{0} = \frac{Q_{0}-A}{B}\]
Plug the solution into the budget equation, we want to solve \(T^{*}\) and \(\Phi\):
(156)#\[\begin{split}\begin{eqnarray}
CT^{*}\omega \cos(\omega t - \Phi) &=& Q^{*}\sin(\omega t) + Q_{0} -(A+B(T_{0}+T^{*}\sin(\omega t - \Phi)))\\
&=& Q^{*}\sin(\omega t) - BT^{*}\sin(\omega t - \Phi)
\end{eqnarray}\end{split}\]
Case \(C=0\).
In this case, the system has no heat capacity. This means that the energy cannot be stored in the system. Everything is in radiative equilibrium.
(157)#\[Q^{*}\sin(\omega t) = BT^{*}\sin(\omega t - \Phi)\]
We can get
(158)#\[\Phi=0, \mbox{ } T^{*}=\frac{Q^{*}}{B} \]
So no heat capacity gives rise to no phase shift. If we assume solar insolation amplitude is about 180 W/m\(^2\) and \(B=2\) W/m\(^2\)/K as before, we can get \(T^{*}=90\) K.
We can arrange the equation to be:
(159)#\[\frac{C\omega}{B}\cos(\omega t - \Phi) + \sin(\omega t - \Phi) = \frac{Q^{*}}{BT^{*}}\sin(\omega t)\]
Let
(160)#\[\tilde{C} = \frac{C\omega}{B}\]
This measures the efficiency of heat storage versus damping of energy anomalies through longwave radiation to space in our system.
Note
The trigonometric identities:
(161)#\[\begin{split}\begin{eqnarray}
\cos(\omega t - \Phi) = \cos(\omega t)\cos(\Phi) + \sin(\omega t)\sin(\Phi)\\
\sin(\omega t - \Phi) = \sin(\omega t)\cos(\Phi) - \cos(\omega t)\sin(\Phi)
\end{eqnarray}\end{split}\]
(162)#\[\frac{Q^{*}}{BT^{*}}\sin(\omega t) = \tilde{C}\cos(\omega t)\cos(\Phi) + \tilde{C}\cos(\omega t)\sin(\Phi) + \sin(\omega t)\cos(\Phi) - \cos(\omega t)\sin(\Phi)\]
(163)#\[\rightarrow \cos(\omega t)(\tilde{C}\cos(\Phi)-\sin(\Phi)) = \sin(\omega t) (\frac{Q^{*}}{BT^{*}}-\tilde{C}\sin(\Phi)-\cos(\Phi))\]
So we can solve the phase shift:
(164)#\[\begin{split}\begin{eqnarray}
\tilde{C}\cos(\Phi)-\sin(\Phi) = 0 \\
\rightarrow \sin(\Phi) = \tilde{C}\cos(\Phi) \\
\rightarrow \Phi = \mbox{arctan}(\tilde{C})
\end{eqnarray}\end{split}\]
And we can solve the amplitude:
(165)#\[\begin{split}\begin{eqnarray}
\frac{Q^{*}}{BT^{*}}-\tilde{C}\sin(\Phi)-\cos(\Phi) = 0 \\
\rightarrow \frac{Q^{*}}{BT^{*}} - (1+\tilde{C}^{2})\cos(\Phi)\\
\rightarrow T^{*} = \frac{Q^{*}}{B(1+\tilde{C}^{2})\cos(\mbox{arctan}(\tilde{C}))}
\end{eqnarray}\end{split}\]
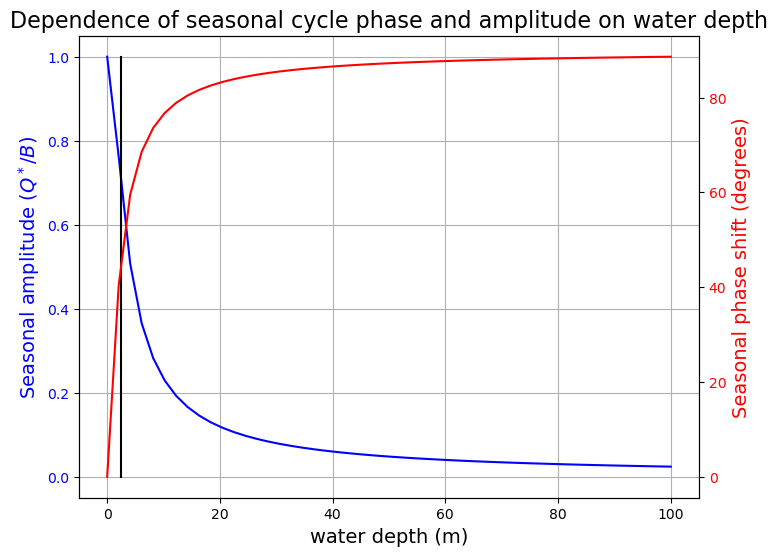
If the water depth is very very shallow:
\(\tilde{C} << 1\)
\(\Phi \approx \tilde{C}\)
\(T^{*} = \frac{Q^{*}(1-\tilde{C})}{B}\)
If the water depth is very deep:
\(\tilde{C} \to\infty\)
\(\Phi \to\ \frac{\pi}{2}\)
\(T^{*} \to 0\)
What are the physical meaning of above results?
The follow-up question is how could we get or estimate reasonalbe heat capacity?
For the atmosphere with specific heat \(c_{p} = 10^{3}\) J/kg/K,
(166)#\[C_{a} = \int_{0}^{p_{s}}c_{p}\frac{dp}{g} \approx 10^{7} \mbox{ J/m$^2$/K}\]
For a well-mixed water with depth 2.5 meters:
(167)#\[C_{w} = c_{w}\rho_{w}H_{w} = 4\times 10^{3}\cdot 10^{3}\cdot 2.5 = 10^{7} \mbox{ J/m$^2$/K} = C_{a}\]
Note
What is \(\tilde{C}\) for a lower boundary of dry land? And what is \(\tilde{C}\) for a 100-meter well-mixed ocean?
omega = 2*np.pi / const.seconds_per_year
print(omega)
B = 2.
Hw = np.linspace(0., 100.)
Ctilde = const.cw * const.rho_w * Hw * omega / B
amp = 1./((Ctilde**2+1)*np.cos(np.arctan(Ctilde)))
Phi = np.arctan(Ctilde)
color1 = 'b'
color2 = 'r'
fig = plt.figure(figsize=(8,6))
ax1 = fig.add_subplot(111)
ax1.plot(Hw, amp, color=color1)
ax1.set_xlabel('water depth (m)', fontsize=14)
ax1.set_ylabel('Seasonal amplitude ($Q^* / B$)', fontsize=14, color=color1)
for tl in ax1.get_yticklabels():
tl.set_color(color1)
ax2 = ax1.twinx()
ax2.plot(Hw, np.rad2deg(Phi), color=color2)
ax2.set_ylabel('Seasonal phase shift (degrees)', fontsize=14, color=color2)
for tl in ax2.get_yticklabels():
tl.set_color(color2)
ax1.set_title('Dependence of seasonal cycle phase and amplitude on water depth', fontsize=16)
ax1.grid()
ax1.plot([2.5, 2.5], [0, 1], 'k-');
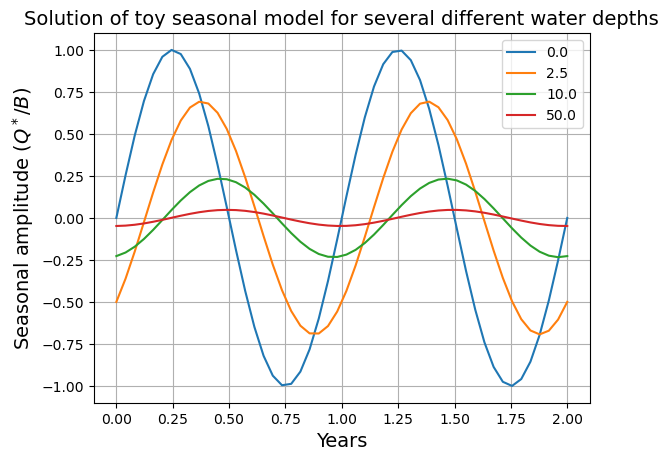
fig, ax = plt.subplots()
years = np.linspace(0,2)
Harray = np.array([0., 2.5, 10., 50.])
for Hw in Harray:
Ctilde = const.cw * const.rho_w * Hw * omega / B
Phi = np.arctan(Ctilde)
ax.plot(years, np.sin(2*np.pi*years - Phi)/np.cos(Phi)/(1+Ctilde**2), label=Hw)
ax.set_xlabel('Years', fontsize=14)
ax.set_ylabel('Seasonal amplitude ($Q^* / B$)', fontsize=14)
ax.set_title('Solution of toy seasonal model for several different water depths', fontsize=14)
ax.legend(); ax.grid()
1.991063797294792e-07
Adding heat transport back to EBM#
(168)#\[C(\phi)\frac{\partial T_{s}}{\partial t} = (1-\alpha(\phi))Q(\phi) - (A+BT_{s}) + \frac{D}{\cos(\phi)}\frac{\partial }{\partial \phi}(\cos(\phi)\frac{\partial T_{s}}{\partial \phi})\]
To make if more realistic, we assume albedo to be:
(169)#\[\alpha(\phi) = \alpha_{0} + \alpha_{2}P_{2}(\sin\phi)\]
# for convenience, set up a dictionary with our reference parameters
param = {'A':210, 'B':2, 'a0':0.354, 'a2':0.25, 'D':0.6}
print(param)
# We can pass the entire dictionary as keyword arguments using the ** notation
model1 = climlab.EBM_seasonal(**param, name='Seasonal EBM')
print(model1)
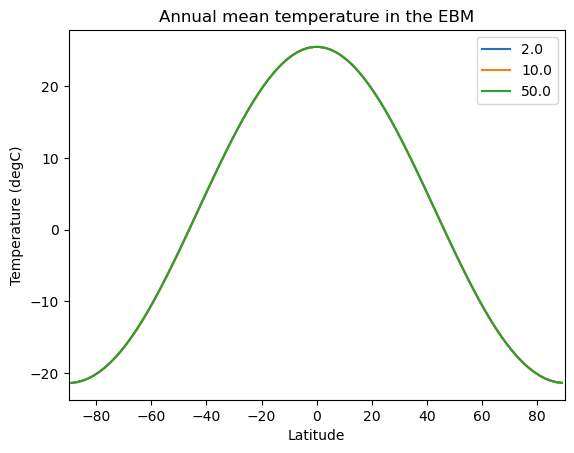
# We will try three different water depths
water_depths = np.array([2., 10., 50.])
num_depths = water_depths.size
Tann = np.empty( [model1.lat.size, num_depths] )
models = []
for n in range(num_depths):
ebm = climlab.EBM_seasonal(water_depth=water_depths[n], **param)
models.append(ebm)
models[n].integrate_years(20., verbose=False )
models[n].integrate_years(1., verbose=False)
Tann[:,n] = np.squeeze(models[n].timeave['Ts'])
lat = model1.lat
fig, ax = plt.subplots()
ax.plot(lat, Tann)
ax.set_xlim(-90,90)
ax.set_xlabel('Latitude')
ax.set_ylabel('Temperature (degC)')
ax.set_title('Annual mean temperature in the EBM')
ax.legend( water_depths )
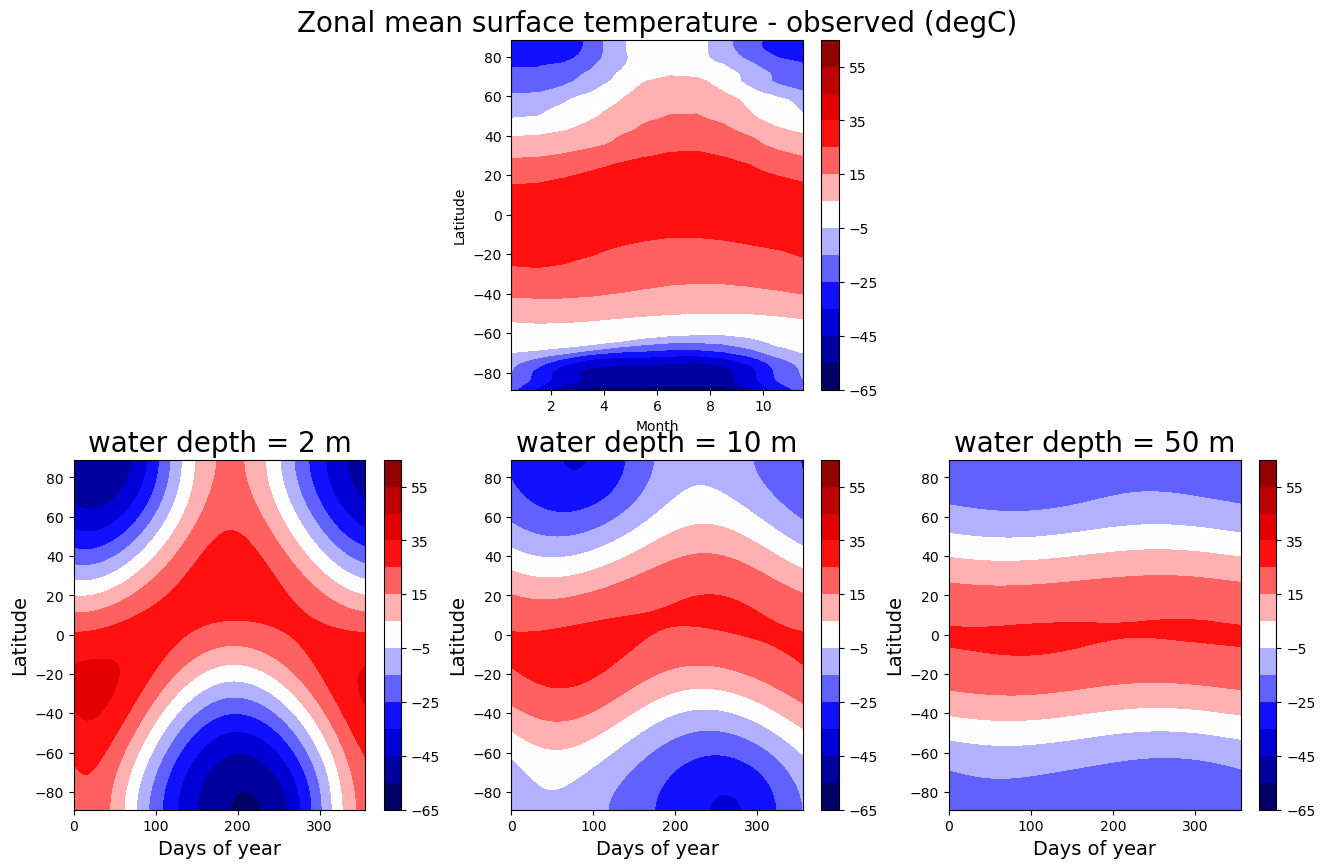
num_steps_per_year = int(model1.time['num_steps_per_year'])
Tyear = np.empty((lat.size, num_steps_per_year, num_depths))
for n in range(num_depths):
for m in range(num_steps_per_year):
models[n].step_forward()
Tyear[:,m,n] = np.squeeze(models[n].Ts)
fig = plt.figure( figsize=(16,10) )
ax = fig.add_subplot(2,num_depths,2)
cax = ax.contourf(np.arange(12)+0.5, lat_ncep,
Ts_ncep.mean(dim='lon').transpose(),
levels=clevels, cmap=plt.cm.seismic,
vmin=Tmin, vmax=Tmax)
ax.set_xlabel('Month')
ax.set_ylabel('Latitude')
cbar = plt.colorbar(cax)
ax.set_title('Zonal mean surface temperature - observed (degC)', fontsize=20)
for n in range(num_depths):
ax = fig.add_subplot(2,num_depths,num_depths+n+1)
cax = ax.contourf(4*np.arange(num_steps_per_year),
lat, Tyear[:,:,n], levels=clevels,
cmap=plt.cm.seismic, vmin=Tmin, vmax=Tmax)
cbar1 = plt.colorbar(cax)
ax.set_title('water depth = %.0f m' %models[n].param['water_depth'], fontsize=20 )
ax.set_xlabel('Days of year', fontsize=14 )
ax.set_ylabel('Latitude', fontsize=14 )
{'A': 210, 'B': 2, 'a0': 0.354, 'a2': 0.25, 'D': 0.6}
climlab Process of type <class 'climlab.model.ebm.EBM_seasonal'>.
State variables and domain shapes:
Ts: (90, 1)
The subprocess tree:
Seasonal EBM: <class 'climlab.model.ebm.EBM_seasonal'>
LW: <class 'climlab.radiation.aplusbt.AplusBT'>
insolation: <class 'climlab.radiation.insolation.DailyInsolation'>
albedo: <class 'climlab.surface.albedo.P2Albedo'>
SW: <class 'climlab.radiation.absorbed_shorwave.SimpleAbsorbedShortwave'>
diffusion: <class 'climlab.dynamics.meridional_heat_diffusion.MeridionalHeatDiffusion'>
Now let’s make an animation.
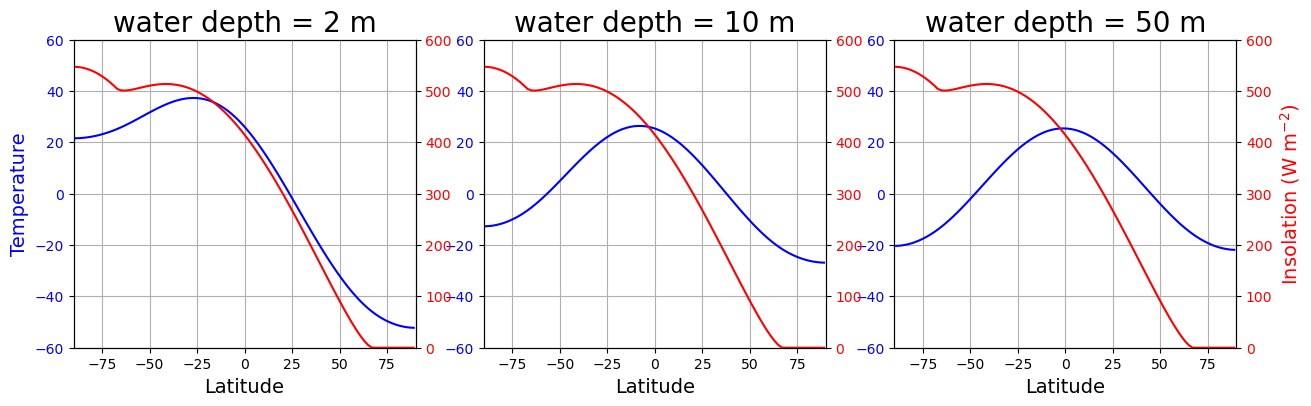
def initial_figure(models):
fig, axes = plt.subplots(1,len(models), figsize=(15,4))
lines = []
for n in range(len(models)):
ax = axes[n]
c1 = 'b'
Tsline = ax.plot(lat, models[n].Ts, c1)[0]
ax.set_title('water depth = %.0f m' %models[n].param['water_depth'], fontsize=20 )
ax.set_xlabel('Latitude', fontsize=14 )
if n == 0:
ax.set_ylabel('Temperature', fontsize=14, color=c1 )
ax.set_xlim([-90,90])
ax.set_ylim([-60,60])
for tl in ax.get_yticklabels():
tl.set_color(c1)
ax.grid()
c2 = 'r'
ax2 = ax.twinx()
Qline = ax2.plot(lat, models[n].insolation, c2)[0]
if n == 2:
ax2.set_ylabel('Insolation (W m$^{-2}$)', color=c2, fontsize=14)
for tl in ax2.get_yticklabels():
tl.set_color(c2)
ax2.set_xlim([-90,90])
ax2.set_ylim([0,600])
lines.append([Tsline, Qline])
return fig, axes, lines
def animate(step, models, lines):
for n, ebm in enumerate(models):
ebm.step_forward()
# The rest of this is just updating the plot
lines[n][0].set_ydata(ebm.Ts)
lines[n][1].set_ydata(ebm.insolation)
return lines
# Plot initial data
fig, axes, lines = initial_figure(models)
# Some imports needed to make and display animations
from IPython.display import HTML
from matplotlib import animation
num_steps = int(models[0].time['num_steps_per_year'])
ani = animation.FuncAnimation(fig, animate,
frames=num_steps,
interval=80,
fargs=(models, lines),
)
HTML(ani.to_html5_video())
Homework assignment X (due xxx)#
Try below example and discuss the results.
orb_highobl = {'ecc':0.,
'obliquity':90.,
'long_peri':0.}
print( orb_highobl)
model_highobl = climlab.EBM_seasonal(orb=orb_highobl, **param)
print( model_highobl.param['orb'])
Tann_highobl = np.empty( [lat.size, num_depths] )
models_highobl = []
for n in range(num_depths):
model = climlab.EBM_seasonal(water_depth=water_depths[n],
orb=orb_highobl,
**param)
models_highobl.append(model)
models_highobl[n].integrate_years(40., verbose=False )
models_highobl[n].integrate_years(1., verbose=False)
Tann_highobl[:,n] = np.squeeze(models_highobl[n].timeave['Ts'])
Tyear_highobl = np.empty([lat.size, num_steps_per_year, num_depths])
for n in range(num_depths):
for m in range(num_steps_per_year):
models_highobl[n].step_forward()
Tyear_highobl[:,m,n] = np.squeeze(models_highobl[n].Ts)
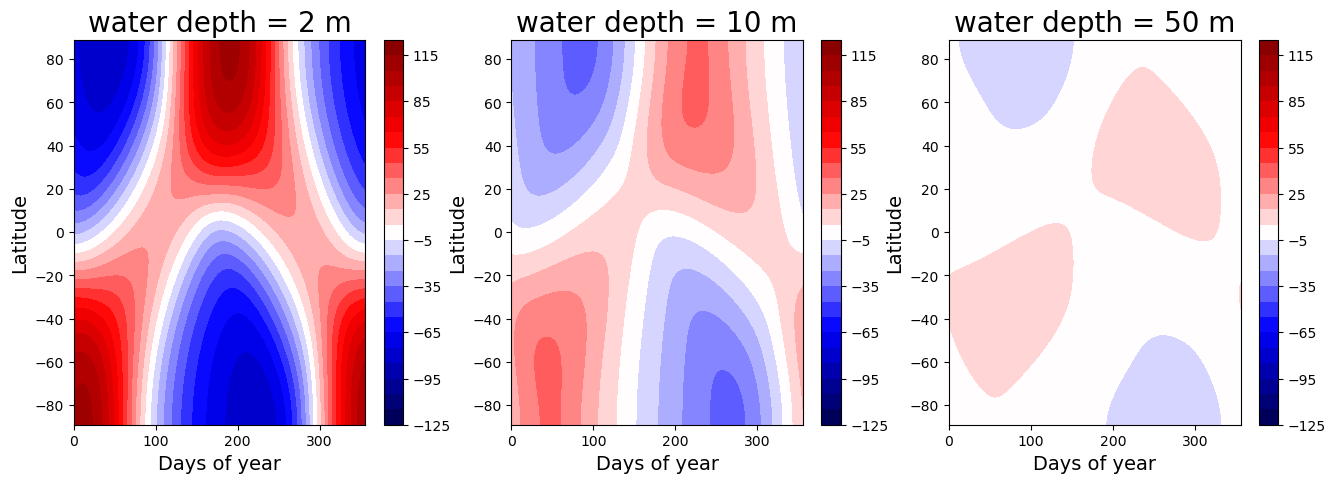
fig = plt.figure( figsize=(16,5) )
Tmax_highobl = 125; Tmin_highobl = -Tmax_highobl; delT_highobl = 10
clevels_highobl = np.arange(Tmin_highobl, Tmax_highobl+delT_highobl, delT_highobl)
for n in range(num_depths):
ax = fig.add_subplot(1,num_depths,n+1)
cax = ax.contourf( 4*np.arange(num_steps_per_year), lat, Tyear_highobl[:,:,n],
levels=clevels_highobl, cmap=plt.cm.seismic, vmin=Tmin_highobl, vmax=Tmax_highobl )
cbar1 = plt.colorbar(cax)
ax.set_title('water depth = %.0f m' %models[n].param['water_depth'], fontsize=20 )
ax.set_xlabel('Days of year', fontsize=14 )
ax.set_ylabel('Latitude', fontsize=14 )
lat2 = np.linspace(-90, 90, 181)
days = np.linspace(1.,50.)/50 * const.days_per_year
Q_present = climlab.solar.insolation.daily_insolation( lat2, days )
Q_highobl = climlab.solar.insolation.daily_insolation( lat2, days, orb_highobl )
Q_present_ann = np.mean( Q_present, axis=1 )
Q_highobl_ann = np.mean( Q_highobl, axis=1 )
{'ecc': 0.0, 'obliquity': 90.0, 'long_peri': 0.0}
{'ecc': 0.0, 'obliquity': 90.0, 'long_peri': 0.0}
